One of the great riddles that has vexed D&D players for generations is this: why did armor class in original D&D descend from 9 to 2 instead of increasing as it gets better? The answer is spelled out in the first draft of D&D: if you were a first-level fighter rolling to hit, the number you needed was equivalent to 20 minus the armor class of your target. To hit AC 2, you needed an 18, to hit AC 3, a 17, and so on. Armor class descended to make it easy enough to calculate your needed roll that you wouldn't even have to consult a table. Unfortunately, the published D&D game broke this algorithm, which has obscured the motivation for descending armor class ever since.
The pre-publication D&D system stipulated that an entry level fighter has only a ten percent chance to land a hit on a target wearing plate armor and a shield. With each level you went up, that likelihood would increase by five percent: so a second-level fighter needs a 17 to hit AC 2, a third-level fight needs a 16, and so on. Presumably that calculation still remained easy enough to perform that this all served as something like a precursor to THAC0 (in its relentless quest to perfect combat systems, the OSR has previously recognized this as the rough algorithm behind the original attack matrices).
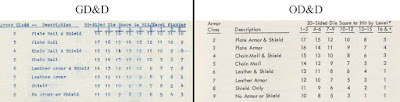
If this system was so intuitive, why didn't TSR stick with it? The most obvious reason is that the attack matrix in the GD&D draft was limited to attackers level 1 through 9, so it can afford to dedicate a column to each level. The attack matrix in published D&D, however, goes up to level 16 and beyond -- so to keep a manageable number of columns in the table, they consolidated levels 1 through 3 of the original attack matrix into a single column. The average of the values in GD&D for the first three levels is 17, and that is the number we see in the first consolidated column of the published D&D chart. Things drift a bit from there: the average of levels 4 through 6 in GD&D would be 14; that has been skewed to 15 in published D&D. No doubt this drift owed to the fact that when you nearly double the number of levels, you need to slow the progression so it isn't too easy for high-level characters to hit. With this consolidation, the original elegance of armor class was instantly lost, and the rationale for the original design was hopelessly obfuscated. This broken remnant of pre-publication D&D cast a long shadow over Holmes Basic and the 1st and 2nd editions of AD&D.
We know that "armor class" was originally a Chainmail term, and Chainmail attached numerical values ascending from 1 to 8 to its armor classes, so that as the armor class of targets went up, likewise did the rolls required to hit them with missile fire. Those eight Chainmail armor classes are transposed exactly into the eight armor classes of OD&D: apart from swapping the order of "Shield Only" and "Leather Armor," the only change is that they are numbered 9 to 2 instead of 1 to 8. But in Chainmail you roll 2d6 to hit, so moving to a d20 to-hit roll (where better rolls are higher) would require something different. In a 1979 interview with Gryphon magazine, Gygax explained, "The concept of armor class and weapon size originated in Chainmail. When I put it into Dungeons & Dragons I just reversed the order of armor class."
But attributions for design choices in original D&D are rarely uncontroversial. In a number of interviews, Arneson credited an unidentified naval wargame involving ironclads as an inspiration for armor class and other early combat system elements. Since the armor classes of D&D are obviously identical to those in Chainmail apart from their ordering, we may be at a bit of a loss to isolate what about armor class this ironclad game could have inspired -- if not the descending values. Arneson's remarks understandably sparked a manhunt for candidate systems with the right age and properties. I was one of many people who, having scoured the fossil records of gaming for the answer, asked Arneson which system he meant, exactly, to no avail. It is true in general that the concepts of armor thickness and withstanding points of damage existed in several naval wargames prior to Chainmail, but less clear which system(s) could have inspired the authors of D&D to alter the armor system in Chainmail to look the way it does in GD&D.
If we accept the rationale for descending armor class given in GD&D draft, then the relevant properties we'd be looking for in a naval game just got much more narrow. That's because reversing the numbers was no mere cosmetic change, but a change made for the very specific purpose of simplifying the calculation of to-hit rolls yielding a number from 1-20. While many pre-D&D to-hit systems used percentile resolution, with dice or cards, prior systems based on rolling 1-20 to hit are exceptionally rare. Given the specific way that "funny dice" got attached to D&D, there are only so many places to look for potential influences.





Wonder of wonders! It is one of the most asinine systems in a book full of asinine systems. It's a wonder that so many players eventually came to a consensus and shaped the system into something coherent. If not exactly the most fun additional roll.
ReplyDeleteUnless I'm misunderstanding something, this doesn't really explain anything. The system of low THAC0, low AC better vs high BAB, high AC better are mathematically equivalent. There's no difference in the systems mathematically.
ReplyDeleteFurther, the shift from GD&D where there are regular THAC0 gains to OD&D where they stagger THAC0 gains doesn't change the underlying system at all (each AC change of 1 requires a roll difference of 1), just that your THAC0 changes at different levels by different increments.
So, the ultimate reason for descending AC isn't any different than it was before: Because Gary arbitrarily choose to do it that way as opposed to a probabilistically identical ascending AC system.
It explains that in the original to-hit system, the table was a perfect progression of -1 per step in either the horizontal or vertical direction. The OD&D table is a mess that does not allow you to derive its values from any mathematical formula we could expect players to embrace as an optimization.
DeleteI did link a post from Delta above which illustrates, to your point, that OSR folks have long recognized that a system that worked cleanly this way would be mathematically equivalent to THAC0. What is news here is that GD&D actually worked cleanly this way, and that indeed the draft text called out the specific calculation that the authors of D&D wanted to enable you to execute as a motivation for the design. That historical motivation is not obvious from studying the OD&D tables, and this has led people to speculate all sorts of other reasons why armor class was organized this way.
Even given that in GDnD the table worked in increments of 1 in both dimensions, that can still be done just as well with an increasing as opposed to decreasing AC. In fact, if you set your target numbers for AC at the right point, it even does it much easier with Roll+Lvl = AC you hit.
DeleteSo this still does not "explain" decreasing AC.
Hang on. I think I'm hung up on the title: "Why did AC descend from 9 to 2?" Whereas if I'm reading you right in your reply here, the main thrust isn't really that, but how nicely the original table worked and how Oe messed it up?
DeleteSo this is answering a historical "why" not a mathematical "why." No evidence we unearth could ever show that of two mathematically equivalent ways of doing things, one has some benefit over the other - a choice between two mathematically equivalent things will always be arbitrary in the sense you seem to be driving at.
DeleteWhat is new here, again, is that GD&D preserves a design rationale, a reason why you use low AC numbers for things that are hard to hit: because the system was "deduct the [AC] number from twenty, and the base number to hit is obtained". OD&D does not obey this formula, and studying OD&D, that original rationale cannot be reverse engineered from its attack table - instead we're just left with descending AC numbers that don't let you calculate your needed rolls, they are just indexes to columns in the table. Studying GD&D reveals that lost motivation for why they descended in the first place.
Alright. Thanks for the clarification. Very interesting read and insight. :)
DeleteMathematically equivalent isn't experientially equivalent.
DeleteI'll give you a third mathematical equivalent, using descending AC(DAC), which is clearly less useful in game:
1d20 less than or equal to DAC + Attacker's Mods
This does the same math as 1d20 + mods greater than or equal to 20-AC, but it prevents hiding the AC of the target, while 1d20 + Mods >= 20-AC allows a concealed TN.
THe other aspect is the hidden BAB equivalent. It's one less modifier for the player, at the expense of 1 more lookup for the GM. I honestly prefer BAB & ascending because the math is faster to do.
Plus, there are educational issues. Generally, scores are given in «higher is better» format. So there's a bias there. I know that by 6th grade, students asked which is better for a game move to succeed, a rule saying "Roll 1 or 2 on a d6" or "Roll 5 or 6 on a d6", over half said 5-6; about a quarter said 1-2. Many had no preference. Of the 90+ students in grades 4-5 I've asked, one preferred "3-4".
Likewise, same age students do additions faster than subtractions with the exact same digits. (A+B=C is faster than C-A=B or C-B=A). Similarly, multiplication is faster than divisions, and more significantly so. (A×B=C is faster than C/A=B or C/B=A.) And remaindered divisions are slower still, as most do not rote memorize them. (As of 6 years ago, the district in which I taught still had most schools requiring the 1-10 multiplication facts as a memorization task in grade 4.)
I've not tested, but my experience as a GM tends to show the same is true for the high school graduates I've been GMing for. I gave up on Rolemaster because it basically required my players to use calculators to get any speed.
Interesting. I always thought the 9 to 2 range must have been the artefact of an earlier 2d6 roll-under system. The probabilities are sensible: you would have to roll under 9 to hit an unarmed combatant, a 83.33% probability; chain would require a 5 (27.77%), and to hit plate and shield with its AC of 2, you would have a measly 2.77%, making an armoured knight practically invincible for normal combatants.
ReplyDeleteIn such a system, attack bonuses or a +1 sword would be major assets, way more powerful than under the standard combat system and the swingy d20.
However, this might have no historical foundation - even if it does make some sense. (Once you switch over to an attack matrix, it does not matter how you call the armour *classes* - they might as well be the original numbers, alphabetical values or any arbitrary code.)
Well, if we believe the stated motivation in the draft, then it's the assumption of a base 10% chance of hitting a fully armor target, combined with a mapping that 10% onto a d20, that set the bottom of the range at 2.
DeleteWho knows if that 10% is an accurate simulation of medieval physics - but once that's your starting point, if you want people to succeed by rolling high, the first number in your chart will be an 18, and armor classes will descend from there.
10% per minute chance of doing significant injury is reasonable for plate with shield, based upon many many reenactors and Armed Renaaissance Martial Arts enthusiasts (and not just the HEMA group), but discounting the SCA. (The SCA's Heavy combat is great for number of hits and for power delivery, but the assumed penetration is not well calibrated, and are based upon chain over gambeson.)
DeleteTHe SCA proves that clubs vs plate are likely only to bruise more than 98% of the time... (I've seen a couple broken toes, a broken finger, and plenty of armor bites from no or too thin a gambeson...)
I’d heard something different on Marv’s d&d discussion board - different naval battle game and different rationale. I don’t want to share it because it would muddy the conversation, but the answer of “why 9 to 2” and it’s origin seemed to fit the facts perfectly.
ReplyDeleteThanks for this great nugget.
If there's a link, throw it up! Won't muddy the conversation.
DeleteThe concept was the smaller the target the harder it is to hit. The better your armor gets, the smaller the openings to your soft spots. Hence it is harder to hit. That's how I always saw it.
ReplyDeleteIt's interesting that Gygax started with +1 THAC0 per level for fighters in the first D&D draft, abandoned it in the published version, and then returned to it (but only as an optional rule) in AD&D. AD&D also returns to a 1st level fighter needing an 18 to hit AC 2 (whereas in published D&D they only need a 17). So the GD&D table is actually closer to AD&D than to what was published in 1974.
ReplyDeleteThe resemblance has a lot to do with how AD&D groups the levels into columns, two levels at a time instead of three in OD&D, which makes everything more regular.
DeleteFor those with a B/X mentality, it looks like if you take the GD&D Table to the best hit probability on the OD&D Table (hit AC 2 on a 5), then you get a 14th level fighter. . .
ReplyDeleteGood stuff as always Jon thanks.
ReplyDeleteGreat to see more of the GD&D! I'm not quite following the end portion. I assume the first two images are the cover and table of contents of the same ruleset, and you think this is the one that influenced them. But how is the hand-written material then related to this? Is it a portion of the same rules that someone (Gygax?) transcribed by hand?
ReplyDeleteNo, sorry, the cover and ToC above are two different rule sets for ironclads that happen to be of the right age. The handwritten one is a page of Arneson's own rules for ironclads, which don't happen to have any armor properties similar to the ones we'd be looking for here.
DeleteYou know what would be even easier than making the AC 2 because you need to roll 18 and 20-2 is 18. Make the AC 18... I'll never understand prefering a system with extra steps...
ReplyDeleteThanks Jon, that explains an annoying aspect of the rules. I like the idea of AC 2 changing to AC 18. It would mean a 1st level fighter wouldn't need a combat table.
ReplyDeleteHow cool to see Target 20 in the pre-publication D&D. But help me out, what am I missing with all the talk of a 10% chance to hit AC 2 for a first level fighter? An 18 or higher on d20 is a 15% chance, no?
ReplyDeleteNo, you're not missing anything. If you squint at the text you'll see someone corrected the 18 to 19 by hand there, but apparently it was too much bother to correct the charts. Math was used... pretty loosely in these designs. Revealing design rationales exposes goofs like this sometimes.
DeleteI remember an old rumor of how Arneson required players to roll over the target number, rather than equal to or over as D&D does it. Perhaps this original to-hit table based based on this "house rule".
DeleteNow I am conufed. I'm not following what Scott or Jon are saying here.
DeleteThe text snippet shown first says the system utilizes a 20-sided die using increments of 5%. That is usually understood as:
1 = 5%
2 = 10%
3 = 15%
4 = 20%
5 = 25%
6 = 30%
7 = 35%
8 = 40%
9 = 45%
10 = 50%
11 = 55%
12 = 60%
13 = 65%
14 = 70%
15 = 75%
16 = 80%
17 = 85%
18 = 90%
19 = 95%
20 = 100%
The text snippet goes on to say that the basis of the system is that of a man (assuming Level 1) attacking requires an 18 (90%) or better to hit an opponent in plate and shield (AC 2). Looking above an 18 on a d20 =90% just as the text snippet originally said.
The text snippet goes on to give an example of 2 - 20 = 18. The math is correct and the lower down from GD&D shows a 18 is needed for level 1 attacking AC 2. So, what is up with the 19, which would be 95%? It seems like the person who changed the number to 19 (Dave, Gary, someone else?) was trying to steer things to “over” rather than “equal to or over.”
What am I missing?
Great find, thanks for posting this. Also, thank you for the OSR shout-out/link!
ReplyDeleteHuh. That's interesting.
ReplyDeleteBut don't forget, we really didn't care about mathematical exactitude. None of us cared that the published table didn't boil down to a tidy mathematical formula, because the way that Dave, and Gary, and all the rest of us did things was "Make up some numbers that look about right, and then diddle with it until it plays as desired."
That's why the magic user XP table is the way it is. Gary changed it several times until he liked it.
Play was paramount.
What became the problem was the system of magic that would supplement fantasy hand-to-hand combat, particularly for higher level PCs where compliments of magic "bonuses" could be several. When does a PC add his/her prescribed magic bonuses into a melee, and is it a minus or plus for the current event? New systems are invented and founded how the old system continued to play with idiosyncrasies affecting easy outcome generation. Note that if a party is really big, all sorts of things could be happening.
ReplyDeleteIn the playtest version of D&D, "The Greyhawk Castle Compaign," Gary was sometimes changing over his rule assessments, and oftentimes adding additional rules after the event. Why? This was before the original D&D was ever released. Gary knew exactly what was required for the original version of the game that had several supplements, including "Gods, Demi-Gods & Heroes." Refining the system was, and still is, a mark of an growing, exceptional product!
What does the ‘G’ stand for in GD&D? Gary, Greyhawk, or general? Interesting article.
ReplyDeleteIn OD&D, the attack tables include a 1 for some of the higher levels. Does this mean no attack roll is needed, since even rolling 1 is a success? Or does it mean attack rolls need to be higher than the numbers indicated on the chart? Like "roll higher than a 1" or "roll higher than a 17" as opposed to "roll a 17 or higher"?
ReplyDeleteFurther to kungfuspacebarbarian’s comment the monster attack table contains both 1s and a single 0! Needing to roll higher would certainly explain this, but the next definitely implies rolling equal…
ReplyDelete